Day: Jun 27, 2020

Stochastic and Non stochastic Quantities 1.1.1

ThirumuruganLeave a comment

Let us consider a system, The system in itself is not a stochastic or non stochastic one. We define a system to be Stochastic or to be deterministic, thus it can be used to measure the physical quantities in it. In Deterministic model we assume we know everything that’s happening in the system and it can be measured using mathematical formulae and equations.

In case of Stochastic model the events happens in a random nature, Hence we find the probability distribution of the event in a particular time interval because the values vary discontinuously in space and time. The value obtained will be in some range with given probability

Where it is useful in ionizing radiation Fields 💡

The fundamental quantities in ionizing radiation are defined based on whether the process of measuring is stochastic or deterministic process

A few example of stochastic quantities defined in ICRU 85 are Energy imparted, lineal energy , specific energy, energy deposit , Where as the absorbed dose is point quantity(i.e. deterministic)

The Radioactive decay is a stochastic process, where it follows Poisson distribution which is uniquely determined by its mean value

To know more about Poisson distribution of radioactive decay refer this document by MIT click here to download and for further reading about Poisson distribution click here

Characteristics of stochastic quantity

  • Value/ events occurs randomly and cannot be predicted. It is determined by a probability distribution (e.g. Poisson distribution in case of radioactive decay)
  • It is defined for finite domains only, Its values vary discontinuously in space and time. so they do not have any gradient or rate of change
  • The values are found with a small uncertainty for a given probability
  • The expectation values Xe is the measure of its mean XÌ„ for n observations. as the n observation approaches ∞ the XÌ„ → Xe

Characteristics of Non-stochastic quantity

  • can be predicted using mathematical equations and formulae
  • It is generally a point function (e.g. absorbed dose). i.e. it has infinitesimal volumes, hence it is differentiable in space and time, rate of change can be obtained
  • Its value is equal to or based upon the expectation value of related stochastic quantity if one exist or they may not be related to stochastic quantity. ( e.g. Specific energy to absorbed dose where the mass is infinitesimal which we will discuss shortly)

Example

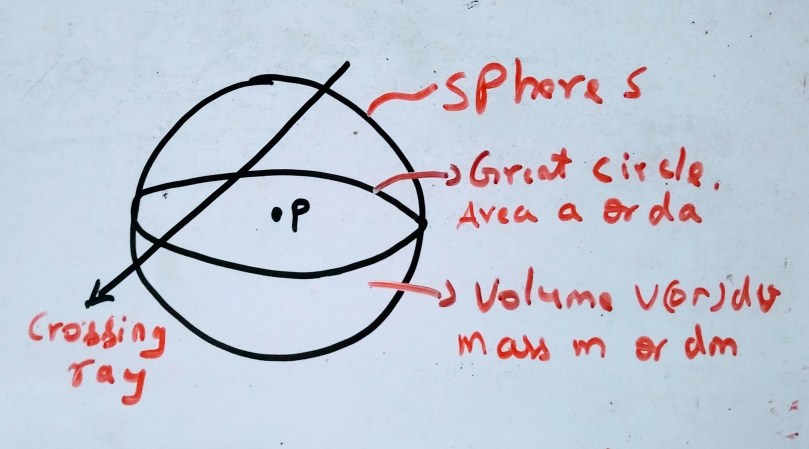
We know from the characteristics of the stochastic quantity, we need to consider a finite domain. In this case we consider a sphere because it has same cross sectional area for rays entering from any direction. Let us consider the specific energy(z), which is the quotient of energy imparted ε to the mass m, the repeated measurements will give the probability distribution of z and its mean z̄ and as the mass becomes infinitesimal dm as mentioned above in the illustration the mean z̄ approaches to absorbed dose D. (the distribution of z is actually not necessary for the measurement of D)

for example in case of biological cell it deals with micro dosimetry, where the knowledge of distribution z corresponding to a know D is important in the irradiated mass m, as the effect of radiation is more closely related to z than D. The values of z greatly differ from D for a small m

If we assume the radiation field is strictly random, as shown from above illustration the rays reaching the given point per unit area and time interval will follow Poisson distribution, for large number of events it may be approximated to Gaussian distribution

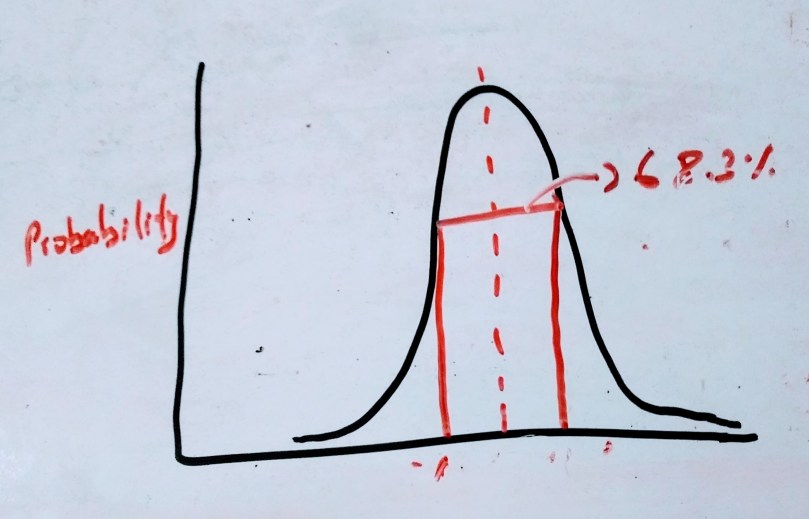
The standard deviation of single random measurement N relative to Ne is equal to σ = \sqrt{N_e} \cong \sqrt{N} and the corresponding percentage deviation is S = \frac{100}{\sqrt{N}} the single random measurement will have probability of true value falling within the uncertainty range is 68.3%

References