Day: Aug 26, 2020

Radioactive decay law

ThirumuruganLeave a comment

Radioactive decay is a stochastic process i.e. probabilistic in nature. In simple words, if we have just one unstable atom we will not know when that atom will disintegrate. But when we have a very large number of unstable atoms of same species, The decay can be estimated using probability distribution i.e. we can say with certain probability that a certain amount of radioactive nuclei will decay in a certain amount of time.

There are various modes of radioactive decay i.e. Alpha decay, beta decay and gamma decay. Though all these modes of decay are different in various aspects including the reason that causes the decay , however the number of particles that changes with time are similar for all these modes of decay.

Radioactive decay law
Here we address about single radioactive substance that’s undergoing radioactive decay to a stable daughter nucleus.

N0 is the number of unstable atoms present at time t = 0
N is the number of atoms present at time t

The number of atoms disintegrating per unit time(dN/dt) is directly proportional to number of atoms present at a give time (N)

\displaystyle \LARGE \bf{ \frac{\mathrm{dN} }{\mathrm{d} t} \hspace{0.3cm} \alpha \hspace{0.3cm} N} (eqn 1️)

The more the number of atoms present the higher the decay rate and vice versa

\displaystyle \LARGE \bf{\frac{\mathrm{dN} }{\mathrm{d} t} \hspace{0.3cm} = \hspace{0.3cm}-\lambda N} (eqn 2️)

where \displaystyle \LARGE \lambda is a proportionality constant (Decay constant or decay probability)
Decay probability is the probability with which any of the N radionuclides will decay.
Negative sign indicates that the rate of disintegration decreases with time i.e. the number of atoms reduces.

If we integrate equation 2 for time = 0 to time = t and find number of atoms N at time = t

\displaystyle \huge \bf{\int_{No}^{N} \frac{\mathrm{dN} }{\mathrm{N}} = -\lambda \int_{0}^{t}dt} (eqn 3)

\displaystyle \huge \bf{\log_{e}(N)-\log_{e}(No) = -\lambda t} (eqn 4)

\displaystyle \huge \bf{\log_{e}(N/No) = - \lambda t} (eqn 5)

from basic rules of logarithm loga (b) = c , where b = ac
In our equation 5, b is nothing but N/No

\displaystyle \huge \bf{\frac{N}{No} = e^{- \lambda t}} (eqn 6)
\displaystyle \huge \bf{N = No \hspace{0.2cm} e^{- \lambda t}} (eqn 7)

Activity

Its is defined as the rate of disintegration. i.e. number of disintegration per unit time. It is given by \displaystyle \huge \bf{ A = - \frac{\Delta N}{\Delta T} = \lambda N}

Similar to the above equation 7 , if Ao is the initial activity at time = 0 and and A is the activity that is to be found at time = t. It is mathematically given as \displaystyle \huge \bf{A = A_0 \hspace{0.2cm} e^{- \lambda t}}

Half Life

The question that raises in our mind when we study about Radioactive decay is why the atoms do not decay in linear fashion. In first half life 50 % of the atoms are decayed and in next half life another remaining 50 percent of atoms are decayed , thus a complete decay happens in 2 half life?

As we discussed earlier the radioactive decay is a random process and from experimental results it is known to follow Poisson statistics. And also the exponential decay curve shows the half life idea more mathematically.
(we do postulate that atoms decay randomly, as it follows Poisson statistics but logically thinking it may or may not be if we think in reverse. Lets wait for some experiments to happen in future which may prove it)

Definition : Half life is defined as the time required for activity or atoms to decay to half of its initial value

From the equation 7 , when N = N0 /2 and t = t1/2 The eqn is written as

\displaystyle \huge \bf{\frac{N_0}{2} = No \hspace{0.2cm} e^{- \lambda t_{\frac{1}{2}}}}

from basic rules of logarithm b = ac —-> c = loga (b)

\displaystyle \huge \bf{- \lambda \hspace{0.1cm} t_{\frac{1}{2}} = \ln (1) - \ln (2)}

as ln(1) = 0 The eqn becomes \displaystyle \huge \bf{- \lambda \hspace{0.1cm} t_{\frac{1}{2}} = - \ln (2)}

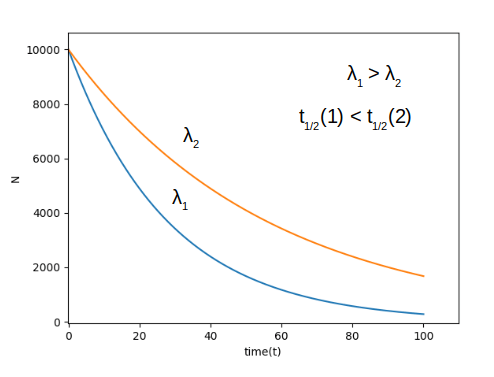
Thus half life is \displaystyle \huge \bf{t_{\frac{1}{2}} = \frac{\ln(2)}{\lambda}}

As the decay constant increases the half life decreases and vice versa, as seen in the above image.

Mean Life

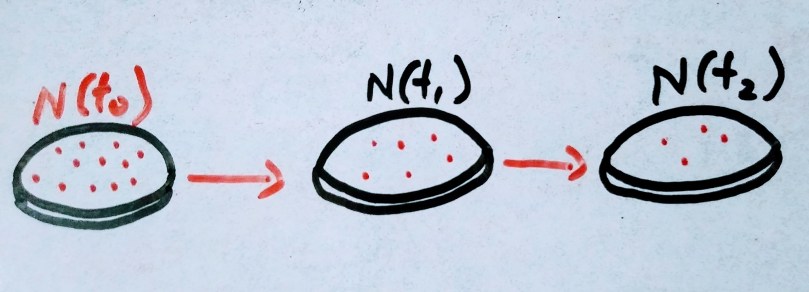
Initially lets consider consider there are 10000 atoms of radioactive elements are there. As humans we always love to think in linear fashion. If 10 atoms decay per second initially and instead of exponential decay , the same 10 decay per second happens until the radioactive atoms vanishes. It would take 1000 seconds to completely decay. And that 1000 second is the mean life of the radioactive element.

It also turns out that mean life = half life / ln(2) . Thus for above problem we can find half life easily , where half life = mean life X ln(2). Answer turns out to be 1000 X 0.69314 = 693.14 seconds.

The Mean or average life Ta is the average lifetime for the decay of radioactive atoms.

\displaystyle \huge \bf{T_{a} = 1 / \lambda = \frac{T_{1/2}}{ln(2)} = 1.44 \hspace{0.2cm} T_{1/2}}

References

1 ) Khan, F. M., & Gibbons, J. P. (2014). Khan’s the physics of radiation therapy. Lippincott Williams & Wilkins.
2 ) math.ucr.edu