Category: blog series

The time scale of effects in radiobiology 🧫

ThirumuruganLeave a comment

The process are divided into three phases

  1. Physical Phase
  2. Chemical Phase
  3. Biological Phase

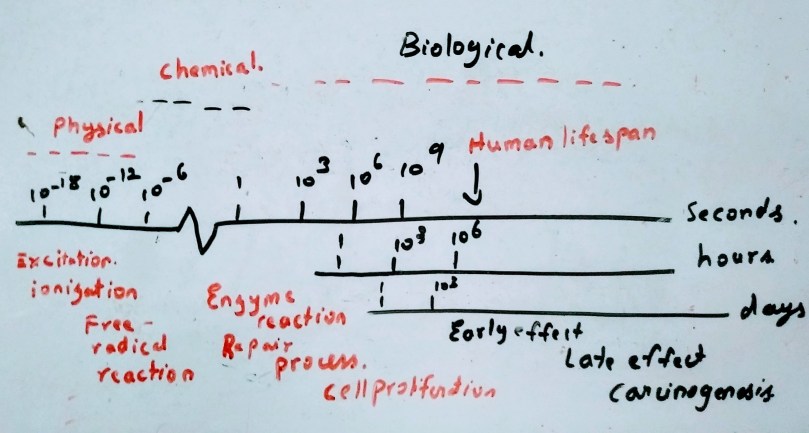
Physical Phase

In physical phase the interaction between the charged particle with the atoms of the tissues occurs. It mainly interacts with orbital electrons, ejecting some of them from atoms while exciting some electrons to higher energy levels. The secondary electrons with sufficient energy can induce further ionization and excitation along the tract(cascade of ionization events). In case of indirect action the fast electrons occurs in approximately 10-15 seconds. A high speed electrons takes about 10-18 seconds to traverse the DNA and 10-14 seconds to traverse the mammalian cells. for the volume of every 10 µm for 1 Gy of absorbed radiation dose almost 105 ionization events occur

Incident X-ray photon
⬇️
Fast electron 10-15 seconds

Chemical Phase

Fast electron
⬇️
Ion radical
⬇️
Free Radical
⬇️
chemical changes from breakage of bonds – 1ms(approx.)

About 80% of the cell in composed of water, when the radiation interacts with water molecules H2O \displaystyle \LARGE \rightarrow H2O+ + e– . the H2O+ ion radical is formed. this ion radical further reacts with H2O to give H3O+ and OH* where OH* is a free radical. Free radical are highly reactive and they will undergo successive reaction to restore the electronic charge equilibrium. The free radical reactions are completed within 1 ms. The important process of chemical phase is the reactions which inactivate the free radicals e.g. reaction with sulphdryl compounds. Then the process of fixation reaction where the stable chemical changes are induced in biologically significant molecules. Here the fixation means not repair, it means that it made sure that the chemical change or damage is permanent.

Biological Phase

Chemical Changes from the breakage of bond
⬇️
Biological effect (days.months,years,
may not happen within human life span)

The biological effect occurs as the consequence of bonds broken. It begins with the enzymatic reaction that occurs on the residual chemical change. While vast majority of the cells repair, few may lead to cell death. 

what is cell death? 
1) loss of specific function - differentiated cells(nerve,muscles,secretory cells) 2) loss of ability to divide - proliferating cells such as stem cells 3) loss of reproductive integrity

During the first few week and months the loss of stem cells due to the radiation is the early manifestation of normal tissue damage and the early effects are also important for tumours as they are early responding tissues.
The secondary effect of cell killing is cell proliferation, which occurs both in tumours as well as normal tissues. for normal tissue it is an important mechanism as it reduces the acute side effect
The late reactions often occur after years of radiation exposure e.g. spinal cord damage, blood vessels damage and radiation carcinogenesis

what is ion radical?

ion means electrically charged and radical means having unpaired electron in valance shell.
H2O \displaystyle \LARGE \rightarrow H2O+ + e–
H2O+ is a ion radical

What is free radical?

Free radicals do not have charge but have unpaired electron in the valance shell.
H2O+ + H2O \displaystyle \LARGE \rightarrow H3O+ + OH*
OH* is the free radical

Reference
Joiner, Michael C., and Albert Van der Kogel. Basic clinical radiobiology fourth edition. CRC press, 2009.

[Most of the sentences written here are taken from basic clinical radio biology book. all credits go the authors of the book mentioned in reference ]

Stochastic and Non stochastic Quantities 1.1.1

ThirumuruganLeave a comment

Let us consider a system, The system in itself is not a stochastic or non stochastic one. We define a system to be Stochastic or to be deterministic, thus it can be used to measure the physical quantities in it. In Deterministic model we assume we know everything that’s happening in the system and it can be measured using mathematical formulae and equations.

In case of Stochastic model the events happens in a random nature, Hence we find the probability distribution of the event in a particular time interval because the values vary discontinuously in space and time. The value obtained will be in some range with given probability

Where it is useful in ionizing radiation Fields 💡

The fundamental quantities in ionizing radiation are defined based on whether the process of measuring is stochastic or deterministic process

A few example of stochastic quantities defined in ICRU 85 are Energy imparted, lineal energy , specific energy, energy deposit , Where as the absorbed dose is point quantity(i.e. deterministic)

The Radioactive decay is a stochastic process, where it follows Poisson distribution which is uniquely determined by its mean value

To know more about Poisson distribution of radioactive decay refer this document by MIT click here to download and for further reading about Poisson distribution click here

Characteristics of stochastic quantity

  • Value/ events occurs randomly and cannot be predicted. It is determined by a probability distribution (e.g. Poisson distribution in case of radioactive decay)
  • It is defined for finite domains only, Its values vary discontinuously in space and time. so they do not have any gradient or rate of change
  • The values are found with a small uncertainty for a given probability
  • The expectation values Xe is the measure of its mean X̄ for n observations. as the n observation approaches ∞ the X̄ → Xe

Characteristics of Non-stochastic quantity

  • can be predicted using mathematical equations and formulae
  • It is generally a point function (e.g. absorbed dose). i.e. it has infinitesimal volumes, hence it is differentiable in space and time, rate of change can be obtained
  • Its value is equal to or based upon the expectation value of related stochastic quantity if one exist or they may not be related to stochastic quantity. ( e.g. Specific energy to absorbed dose where the mass is infinitesimal which we will discuss shortly)

Example

We know from the characteristics of the stochastic quantity, we need to consider a finite domain. In this case we consider a sphere because it has same cross sectional area for rays entering from any direction. Let us consider the specific energy(z), which is the quotient of energy imparted ε to the mass m, the repeated measurements will give the probability distribution of z and its mean z̄ and as the mass becomes infinitesimal dm as mentioned above in the illustration the mean z̄ approaches to absorbed dose D. (the distribution of z is actually not necessary for the measurement of D)

for example in case of biological cell it deals with micro dosimetry, where the knowledge of distribution z corresponding to a know D is important in the irradiated mass m, as the effect of radiation is more closely related to z than D. The values of z greatly differ from D for a small m

If we assume the radiation field is strictly random, as shown from above illustration the rays reaching the given point per unit area and time interval will follow Poisson distribution, for large number of events it may be approximated to Gaussian distribution

The standard deviation of single random measurement N relative to Ne is equal to σ = \sqrt{N_e} \cong \sqrt{N} and the corresponding percentage deviation is S = \frac{100}{\sqrt{N}} the single random measurement will have probability of true value falling within the uncertainty range is 68.3%

References